库伦定律
目录
1 探究影响电荷之间相互作用力的因素
- 实验现象:
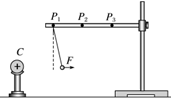
- 小球带电荷量一定时,距离带电物体越远,丝线偏离竖直方向的角度越小.
- 小球处于同一位置时,小球所带的电荷量越大,丝线偏离竖直方向的角度越大.
- 实验结论: 电荷之间的作用力随着电荷量的增大而增大,随着距离的增大而减小.
2 点电荷
- 定义: 如果带电体本身的线度比相互作用的带电体之间的距离小得多,以致带电体的体积和形状对相互作用力的影响可以忽略不计时,这种带电体就可以看成点电荷。
注意
-
点电荷自身不一定很小,所带电荷量也不一定很少。
-
点电荷是一种理想化的模型。
3 库仑定律
在真空中两个点电荷间的作用力跟它们的电荷量的乘积成正比,跟它们之间的距离的平方成反比,作用力的方向在它们的连线上。
-
公式: $F=k\frac{q_1q_2}{r^2}$,其中$k= \pu{9.0 \times 10^3 N*m2/C2}$为静电力常量.
-
适用条件: 真空中的静止点电荷.
在空气中,两个点电荷的作用力近似等于真空中的情况,可以直接应用公式. 当两个带电体间的距离远大于其本身的大小时,可以把带电体看成点电荷.
- 库仑力的方向: 由相互作用的两个带电体决定,即同种电荷相互排斥,异种电荷相互吸引.
注意
-
两个点电荷之间的相互作用力是一对作用力和反作用力,等大、反向
-
对于两个均匀带电绝缘球体,可将其视为电荷集中在球心的点电荷,$r$为球心间的距离.
-
不能根据公式错误地认为$r\rightarrow 0$时,库仑力$F \rightarrow \infty$,因为当$r\rightarrow 0$时,两个带电体已不能看成点电荷了
-
对于两个带电金属球,要考虑表面电荷的重新分布.

- 同种电荷: $F < k\frac{q_1q_2}{r^2}$
- 异种电荷: $F > k\frac{q_1q_2}{r^2}$
- 两点电荷间的库仑力与周围是否存在其他电荷无关,两个或两个以上点电荷对某一个点电荷的作用力,等于各点电荷单独对这个点电荷的作用力的矢量和.
4 库仑的实验
-
库仑扭秤实验是通过悬丝扭转的角度比较静电力$F$大小的.实验结果发现静电力$F$与距离$r$的二次方成反比.
-
库仑在实验中为研究$F$与$q$的关系,采用的是用两个完全相同的金属小球接触,电荷量平分的方法,发现$F$与$q_1$和$q_2$的乘积成正比.