电场与电场强度
1 电场
带电体周围存在的一种物质,是电荷间相互作用的媒体。
-
电场是客观存在的,电场具有力的特性和能的特性。
-
基本性质:
- 对放入其中的电荷有力的作用。
- 当电荷在电场移动时,电场力能对电荷做功(说明电场具有能量)。
2 电场强度
2.1 场源电荷和试探电荷
-
场源电荷: 激发电场的带电体所带的电荷叫作场源电荷,或源电荷。
-
试探电荷: 用来检验电场是否存在及研究其强弱分布情况的电荷叫作试探电荷或检验电荷。试探电荷电性正负均可。
-
试探电荷满足的条件:
-
体积足够小
-
电荷量足够小,保证它的置入不引起原有电场的电荷重新分布或对原有电场的影响可忽略不计。
-
2.2 电场强度
- 定义: 放入电场中某一点的电荷受到的电场力跟它的电荷量的比值,叫做这一点的电场强度。
- 定义式: $E = \frac{F}{q}$
- 方向:电场强度是矢量,其运算遵循平行四边形定则。电场中某点的电场强度方向与正电荷在该点受静电力的方向相同;与负电荷在该点受静电力的方向相反。
- 物理意义: 表示电场强弱和方向的物理量,在数值上等于单位电荷量的电荷在电场中受到的静电力的大小。
3 点电荷的电场
- 表达式: $E = k \frac{Q}{r^2}$
- 方向: 如果以$Q$为中心作一个球面,当$Q$为正电荷时,$E$的方向沿半径向外;当$Q$为负电荷时,$E$的方向沿半径向内。
- 适用条件: $E = k \frac{Q}{r^2}$仅适用于真空中点电荷的电场,$E = \frac{F}{q}$适用于一切电场。
4 电场强度的叠加
电场强度是矢量,当空间的电场是由几个点电荷共同激发的时候,空间某点的电场强度等于每个点电荷单独存在时所激发的电场在该点的场强的矢量和(叠加时遵循平行四边形定则)。
4.1 电场强度三个表达式的比较
| 表达式 | $E = \frac{F}{q}$ | $E = k\frac{Q}{r^2}$ | $E = \frac{U}{d}$ |
|---|---|---|---|
| 公式意义 | 电场强度定义式 | 真空中点电荷的电场强度决定式 | 匀强电场中E与U的关系式 |
| 适用条件 | 一切电场 | 真空、点电荷 | 匀强电场 |
| 决定因素 | 由电场本身决定, 与检验电荷无关 | 由场源电荷和场源电荷到该点的距离$r$共同决定 | 由电场本身决定,d为电场中两点沿电场方向的距离 |
5 电场线及其特点
电场线是画在电场中的一条条有方向的曲线,曲线上每点的切线方向表示该点的电场强度方向。
- 特点:
- 电场线从正电荷或无限远出发,终止于无限远或负电荷。
- 电场线在电场中不相交。
- 在同一电场中,电场强度较大的地方电场线较密,电场强度较小的地方电场线较疏。
-
电场线是为了形象地描述电场而假想的线,实际上是不存在的。
-
电场线每点的切线方向与该点的电场强度方向相同。
几种特殊的电场线分布,如图所示。
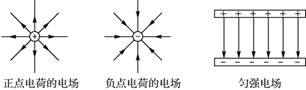
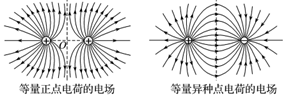
5.1 电场线与带电粒子运动轨迹的关系
-
带电粒子仅在电场力作用下做直线运动的条件:
-
电场线是直线;
-
带电粒子初速度为零或初速度方向与电场线平行。
若粒子初速度不为零,其运动方向与受力方向相同,则粒子做加速运动,反之则粒子做减速运动。
-
-
带电粒子仅在电场力作用下做曲线运动的特点:
-
带电粒子的受力方向指向曲线凹侧;
-
根据受力方向结合粒子电性判断电场强度方向;
-
运动轨迹上某点的切线方向表示粒子在该点的速度方向。
-
6 匀强电场及其特点
如果电场中各点的电场强度的大小相等、方向相同,这个电场就叫作匀强电场。
- 特点:
- 电场方向处处相同,电场线是平行直线。
- 场强大小处处相等,电场线疏密程度相等。
7 特殊电场的场强计算
-
等效法: 在保证效果相同的前提下,将复杂的电场情景变换为简单的或熟悉的电场情景。
例如: 一个点电荷$+q$与一个无限大薄金属板形成的电场,等效为两个异种点电荷形成的电场,如图甲、乙所示。
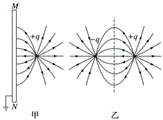
-
对称法: 利用空间上对称分布的电荷形成的电场具有对称性的特点,使复杂电场的叠加计算问题大为简化。
例如: 如图所示,均匀带电的球壳在$O$点产生的场强,等效为$\overset{\LARGE{\frown}}{BC}$产生的场强,$\overset{\LARGE{\frown}}{BC}$产生的场强方向,又等效为弧的中点$M$在$O$点产生的场强方向。
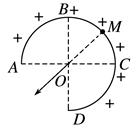
- 填补法: 将有缺口的带电圆环或圆板补全为完整的圆环或圆板,或将半球面补全为球面,从而化难为易、事半功倍。
-
点电荷电场、匀强电场场强叠加一般应用合成法即可。
-
均匀带电体与点电荷场强叠加一般应用对称法。
-
计算均匀带电体某点产生的场强一般应用补偿法或微元法。